신경망의 Weight의 시작 값은 어떻게 해주어야 할까요? 신경망의 Weight값이 모두 0이거나 모두 같으면 문제가 발생합니다. Weight 갱신 시 Gradient가 같아서, Weight가 같은 값으로 갱신되기 때문입니다. ‘곱셈 노드의 역전파 그래프’ 를 떠올리면 이해가 쉽습니다. 각 층이 모두 같은 Weight를 가진다면 미분값이 모두 같게 되겠죠? 초기에는 신경망의 Weight 값을 표준편차가 0.01인 정규분포를 따르는 난수로 초기화 했었습니다만 표현력이 떨어진다는 단점이 있었습니다. 그래서 Xavier초기값과 He 초기값이 나오게 되었습니다. 이에 이르는 과정을 알아봅시다.
표준편차 1인 정규분포로 Weight 초기화
np.random.randn(1000, 100)은 표준편차가 1인 정규분포로 1000×100 행열을 생성합니다. 이것을 1000개 데이터라 가정하고, Weight는 np.random.randn(100, 100) 형태로 생성을 합니다. 그러면 표준편차 1인 정규분포로 신경망이 초기화 된 것 입니다. 활성화함수는 Sigmoid로 해주겠습니다. 이렇게 세팅하고, 신경망에 통과시키면 각 층의 활성화값은 대부분 0과 1이 됩니다. 활성화값이 0과 1이면 Sigmoid 함수에서 기울기 값이 사라지므로 Vanishing Gradient 문제가 발생하게 됩니다.
각 층의 활성화값이 0 또는 1이 대부분을 차지.
그런데 왜? 표준편차가 1인 정규분포로 Weight를 초기화 하면 활성화값이 대부분 0과 1이 될까요?
일단 np.random.randn(1000, 100)으로 생성한 1000개 데이터와 신경망의 1층인 np.random.randn(100, 100) 곱(dot)하면 아래와 같은 분포의 값이 나오게 됩니다.
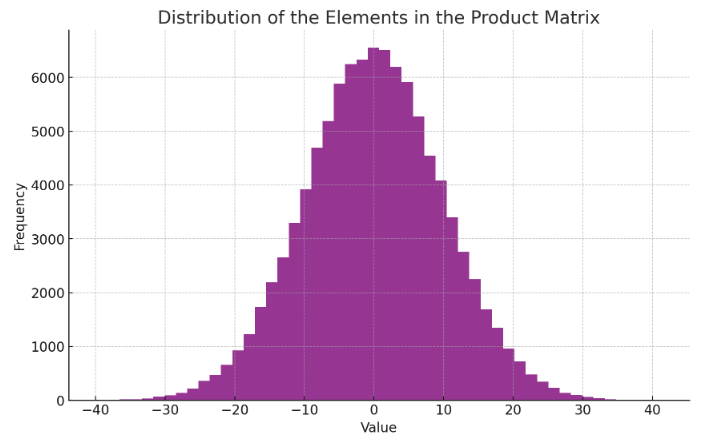
이 값들을 Sigmoid에 통과시키면 -4, 4값에서 0과 1로 포화되는 Sigmoid의 특성상 대부분의 값이 0과 1의 값으로 몰리게 됩니다.
혹시 표준편차가 1인 정규분포로 생성한 데이터와 신경망의 곱의 결과물이 위처럼 분산이 커지는 현상이 잘 이해되지 않는다면, 정규분포를 따르는 값을 곱해서 나온 수들은 이전보다 분산이 커진다 라고 이해하시면 될 것 같습니다.
표준편차가 1인 정규분포로 초기화 하면 안되는 이유
결론적으로 표준편차가 1인 정규분포로 초기화한 데이터와 Weight의 초기값의 곱(신경망통과)을 하면 분산이 커지게 되고, -4와 4에서부터 포화가 되는 Sigmoid 함수의 특성상 각 층의 출력값의 대부분이 0과 1이 되면서 기울기의 값이 작아지다가 사라지는 Vanishing Gradient가 발생하는 것입니다.
그렇다면 표준편차를 더 줄여서 0.01로하면 되지 않을까요? 하지만 표준편차를 0.01로 해서 초기값을 설정하면 활성화값이 0.5에 치우치기 때문에, 노드 100개가 거의 같은 값을 출력하게 되어 노드를 증가시키는 의미가 없어지게 됩니다. 한마디로 표현력이 줄어든다는 의미입니다. 이처럼 파라미터의 초기값을 설정하는 것은 매우 중요합니다.
Xavier 초기값
이러한 한계로 인해 Xavier 초기값이 나오게 되었습니다. 노드의 활성화 값을 적절하게 분포시킬 목적으로 앞계층의 노드 개수의 제곱근을 나눠주면 됩니다.
np.random.randn(node_num, node_num) / np.sqrt(node_num)해당 방법은 Activation Func이 Sigmoid일 때 각 층의 활성화값의 분포를 고르게 해주는 방식이고, 요즘에는 Sigmoid 보다는 ReLU계열을 많이 사용하므로 Weight의 초기값이 조금 다르게 합니다.
He 초기값
ReLU를 활성화 함수로 사용할 경우, He초기값을 많이 사용합니다. 별로 다르지 않습니다. 표준편차를 Xavier방식에서 곱하기 2만 해주면 됩니다. ReLU는 음의 영역이 0이라서 더 넓게 분포시키기위해 2배 해주는 것입니다.